子序列:一个给定序列的子序列就是该给定序列去掉零个或者多个元素后的序列。例如:$Z={B, C, D, B}$是$X={A, B, C, B, D, A, B}$的一个子序列。注意顺序不能改变。
公共子序列:既是序列$X$的子序列,又是序列$Y$的子序列。例如:$X={A, B, C, B, D, A, B}$,$Y={B, D, C, A, B, A}$,则序列 ${B, C, A}$ 是$X$和$Y$的一个公共子序列,长度为$4$;序列${B, C, B, A}$ 是$X$和$Y$的一个最长公共子序列(LCS),长度为$4$.
当然,我们可以查用穷举法来解决问题,但是,对于一个长度为$n$的序列,其子序列为$2^n$,因此时间复杂度为指数形式,当$n$很大时,显然不合实际。由观察和推导可知,最长公共子序列具有最优子结构性质和重叠子问题性质。因此我们可以通过动态规划算法来找到最长公共子序列,其时间复杂度为$O(mn+m+n)$。($m,n$ 分别为两个序列的元素个数)
在下面的程序实现中,我假设两个序列为上面提到的$X={A,B,C,B,D,A,B}, Y={B, D, C, A, B, A}$,数组$b$对应于在计算$c[i][j]$时所选择的最优子问题的解,数组$c[i][j]$为$X_i$和$Y_j$的一个LCS的长度,$X_i$为序列的前$i$个元素组成的序列,$Y_j$为序列的前$j$个元素组成的序列.
具体程序如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
| #include<stdio.h>
void Lcs_Length(char *X,char *Y,int n1,int n2,int b[][7],int c[][7]);
void Print_Lcs(char *X,int b[][7],int i,int j);
void main()
{
char X[]={'A','B','C','B','D','A','B'};
char Y[]={'B','D','C','A','B','A'};
int n1=sizeof(X)/sizeof(char);
int n2=sizeof(Y)/sizeof(char);
int b[8][7]={0};
int c[8][7]={0};
Lcs_Length(X,Y,n1,n2,b,c);
printf("最长公共子序列为:");
Print_Lcs(X,b,n1,n2);
printf("\n");
}
void Lcs_Length(char *X,char *Y,int n1,int n2,int b[][7],int c[][7])
{
for(int i=0;i<n1;i++)
c[i][0]=0;
for(int i=0;i<n2;i++)
c[0][i]=0;
for(int i=1;i<=n1;i++)
for(int j=1;j<=n2;j++)
{
if(X[i-1]==Y[j-1])
{
c[i][j]=c[i-1][j-1]+1;
b[i][j]=1;
}
else if(c[i-1][j]>=c[i][j-1])
{
c[i][j]=c[i-1][j];
b[i][j]=2;
}
else
{
c[i][j]=c[i][j-1];
b[i][j]=3;
}
}
}
void Print_Lcs(char *X,int b[][7],int i,int j)
{
if(i==0||j==0)
return;
if(b[i][j]==1)
{
Print_Lcs(X,b,i-1,j-1);
printf("%c ",X[i-1]);
}
else if(b[i][j]==2)
Print_Lcs(X,b,i-1,j);
else
Print_Lcs(X,b,i,j-1);
}
|
上面程序得到的结果数组$c$和$b$如下图:
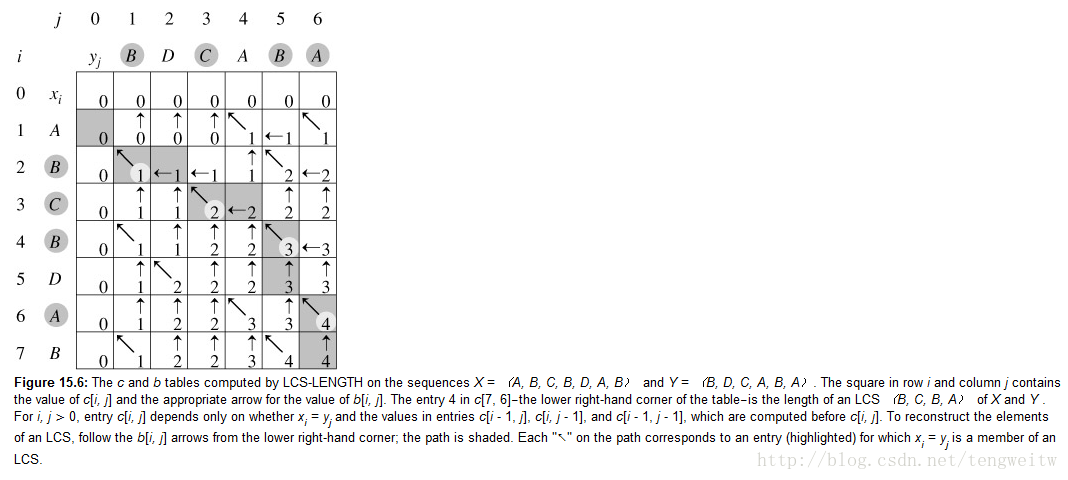
上表中的数字代表长度,例如$c[7][6]=4$代表序列$X$的前$7$个元素组成的序列和序列$Y$前$6$个元素组成的序列的最长公共子序列的长度为$4$.
在程序中为了方便起见,$b$数组用数字$1, 2, 3$分别代表$↖,↑,←$。


